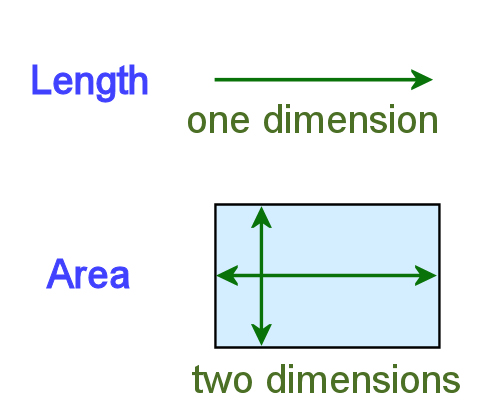
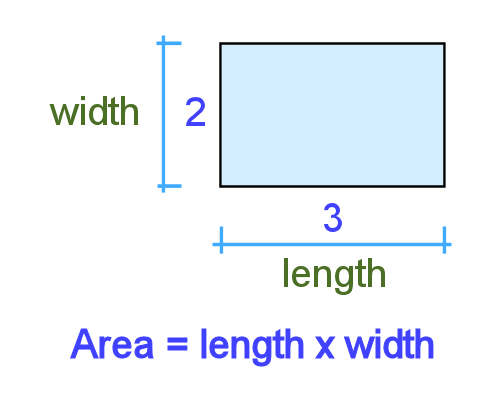
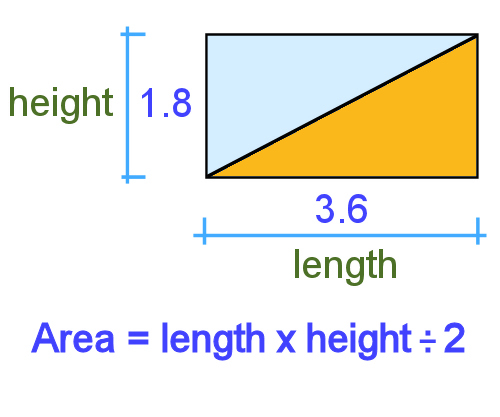
Area
 Audio for slide 5 (mp3 |6|KB)
Audio for slide 5 (mp3 |6|KB)
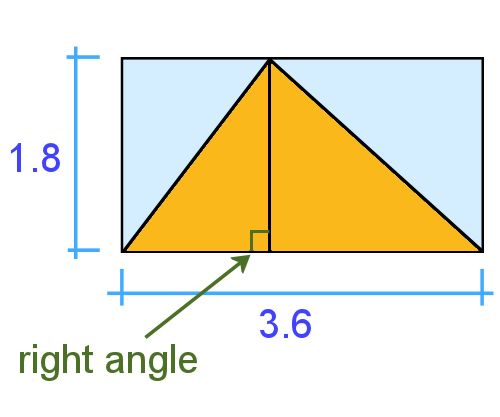
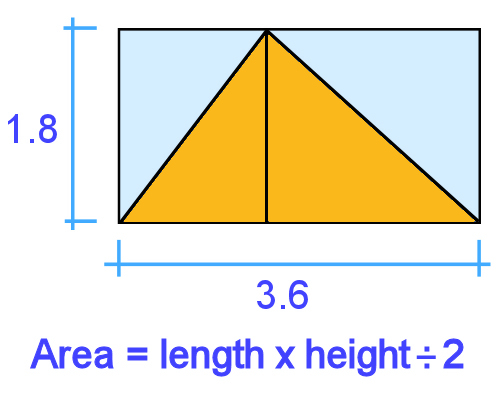
So even if you had a triangle that didn't have a right angle in it, the calculation is still the same, because you could simply divide the triangle into 2 triangles, and the rectangle around it into 2 rectangles.

 Audio for slide 11 (mp3 |6|KB)
Audio for slide 11 (mp3 |6|KB)
Compound shapes
If you can break a shape up into its basic parts, you can calculate its area by adding the separate areas together.
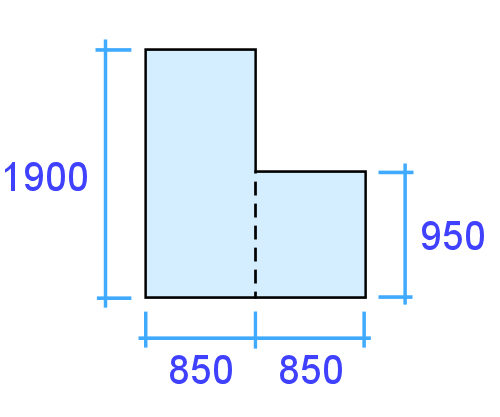
Example 1: L shape
This L shape is basically two rectangles. What is its area? Note that the measurements in the diagram are shown in millimetres, so you'll need to convert them into metres for the calculation. A good way to set out the workings is as follows.
Rectangle 1: 1.9 x 0.85 = 1.615 m²
Rectangle 2: 0.95 x 0.85 = 0.808 m²
Total area: 1.615 + 0.808 = 2.423 m²
Written mathematically, this would be:
(1.9 x 0.85) + (0.95 x 0.85) = 2.423 m²

 Audio for slide 12 (mp3 |6|KB)
Audio for slide 12 (mp3 |6|KB)
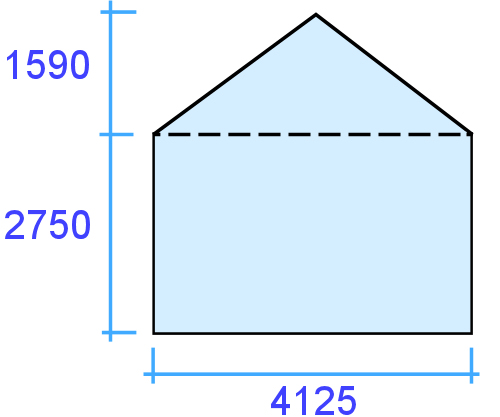
Example 2: Gable end of a house
This shape is a triangle plus a rectangle. Again, you can set out your workings in the same way.
Triangle: 1.59 x 4.125 ÷ 2 = 3.279 m²
Rectangle: 2.75 x 4.125 = 17.05 m²
Total area: 5.58 + 17.05 = 22.63 m²
Written mathematically: (1.8 x 6.2 ÷ 2) + (6.2 x 2.75) = 22.63 m²

 Audio for slide 13 (mp3 |6|KB)
Audio for slide 13 (mp3 |6|KB)
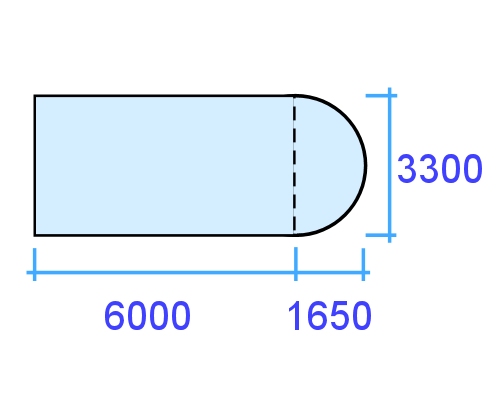
Example 3: Half circle around a bay window
This floor area is made up of a rectangle and a semicircle.
The formulas and calculations for finding this area are as follows:
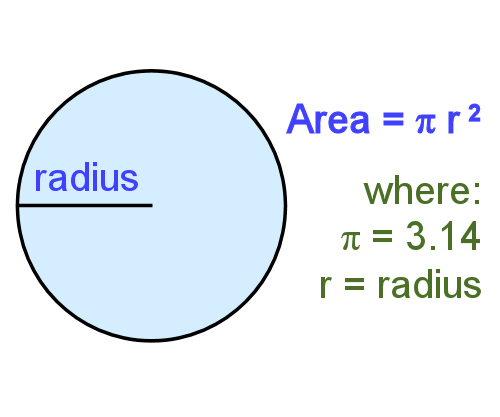
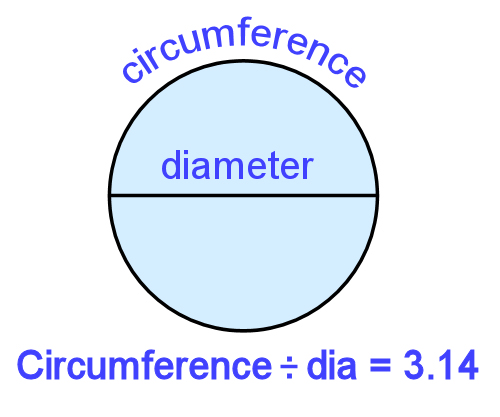
Semicircle area = area of circle ÷ 2.
In other words:
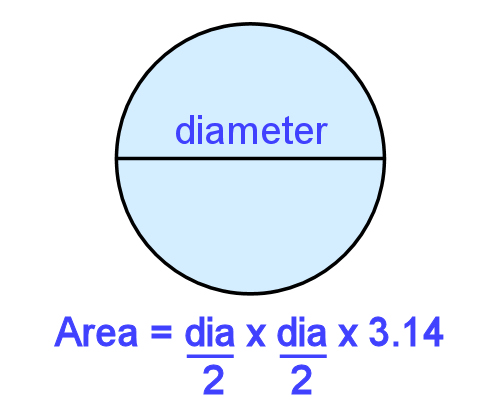
Semicircle = (diameter ÷ 2) x (diameter ÷ 2) x 3.14 ÷ 2
= (3.3 ÷ 2) x (3.3 ÷ 2) x 3.14 ÷ 2
= 1.65 x 1.65 x 3.14 ÷ 2
= 4.274 m2
Now we can do the rest of the calculation:
Rectangle: 6.0 x 3.3 = 19.8 m2
Total area: 4.274 + 19.8 = 24.074 m2
Written mathematically: (3.3 ÷ 2 x 3.3 ÷ 2 x 3.14 ÷ 2) + (6.0 x 3.3) = 24.074 m2


Learning activity
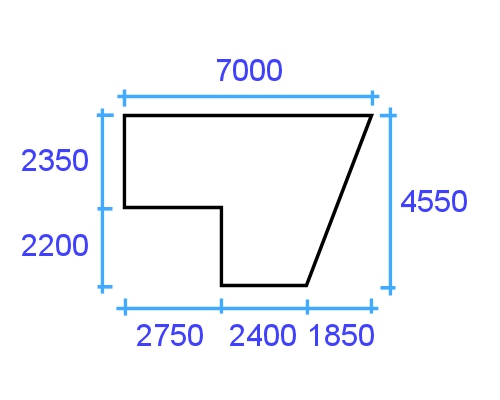
Audio 14 (mp3 |6|KB)You have been asked to measure up the floor area of the house shown below.
What is the total area in square metres?
Enter your answer into the cell, and click on the 'Check your answer' button to see if you were right.

 | 21.59 | m² |
 Go to Angles
Go to Angles