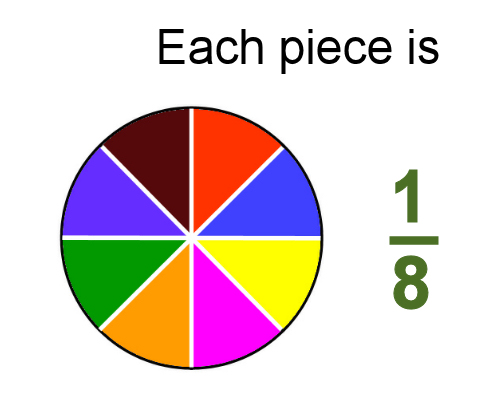Audio for slide 2 (mp3)
Audio for slide 2 (mp3)
The ability to take accurate measurements and use them in calculations is central to the skills of a floor layer. Some people find this sort of 'applied mathematics' easy. Others need to think more carefully about what they're doing to avoid making mistakes.
 Audio for slide 3 (mp3)
Audio for slide 3 (mp3)
But either way, the types of measurements and calculations that floor layers need to do are very practical, and once you understand the principles you can adapt the techniques to any site-specific situation. In this unit we'll look at the mathematical concepts that underpin the work you do with numbers as a floor layer.
 Audio for slide 4 (mp3)
Audio for slide 4 (mp3)
Note that we won't discuss specific types of calculations in detail - these applications are left for the individual units they relate to. However, we will provide the background information you need to know in order to take measurements on-site and use them to solve basic geometric and mathematical questions.
 Audio for slide 7 (mp3)
Audio for slide 7 (mp3)
There are some calculations you can do in your head. Counting items and working out simple quantities are calculations that people do all the time, almost without thinking about it. But as the numbers get bigger or more complex, most people need to use a calculator to be sure that they've got the right result.
 Audio for slide 8 (mp3)
Audio for slide 8 (mp3)
Fortunately, calculators are everywhere these days. You'll find them in mobile phones, on rulers, in large diaries, and of course as self-contained pocket-sized devices.
 Audio for slide 9 (mp3)
Audio for slide 9 (mp3)
In this section, we'll cover some basic calculations and mathematical procedures that you need to know in order to work with numbers. We'll also look at the metric system and discuss the terms that apply to various units of measure.
 Audio for slide 11 (mp3)
Audio for slide 11 (mp3)
If you're having trouble using a calculator, the best advice is to read the manufacturer's instructions. Different calculators operate in different ways, and they don't always follow the same order for entering numbers and functions. Here's a few general hints on how to use a calculator effectively.
 Audio for slide 12 (mp3)
Audio for slide 12 (mp3)
1. Clear the calculator before you start any new calculation. This will ensure that nothing you did before gets mixed up with the calculation you are about to begin
 Audio for slide 13 (mp3)
Audio for slide 13 (mp3)
2. Write down the numbers first if they are complicated. You should also write them down if someone is calling them out to you, such as while taking a series of measurements. Then you can be sure that you're entering the right numbers, especially if they have decimal points or several zeros.
 Audio for slide 14 (mp3)
Audio for slide 14 (mp3)
3. Estimate the answer in your head if the numbers are long or complicated. This will help you to pick up mistakes, because it will give you an idea of the size of the answer you're looking for.
 Audio for slide 15 (mp3)
Audio for slide 15 (mp3)
For example, if you had 18 carpet grippers that were each 1.2 metres long, and you wanted to know what the total metreage was, you could do the following calculation in your head: 20 (rounding up 18) x 1 (rounding down 1.2) = 20 So when you do the actual calculation and find that the answer is 21.6 metres, you'll know that it sounds about right.
 Audio for slide 16 (mp3)
Audio for slide 16 (mp3)
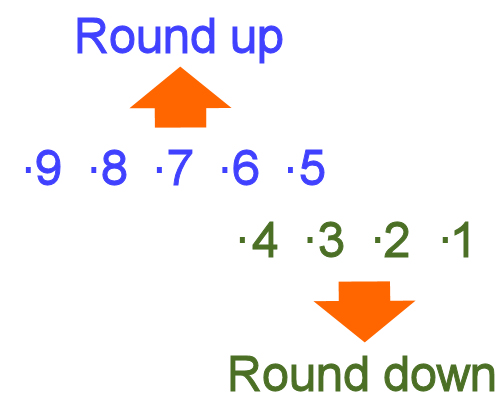
The rule of thumb for rounding off numbers is: Ending in a 5 or more - round up Ending in a 4 or less - round down
 Audio for slide 18 (mp3)
Audio for slide 18 (mp3)
Fractions are made up of two parts. The top part is called the numerator and tells you how many pieces you've got. The bottom part is called the denominator and tells you how many pieces make up the whole.
 Audio for slide 19 (mp3)
Audio for slide 19 (mp3)
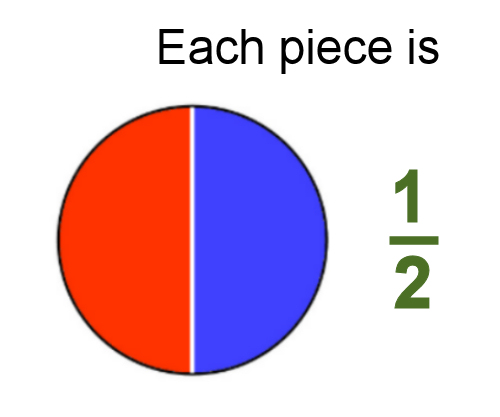
For example, if there are two pieces in the whole, each piece is one half. That is, each piece represents 1/2.
 Audio for slide 21 (mp3)
Audio for slide 21 (mp3)
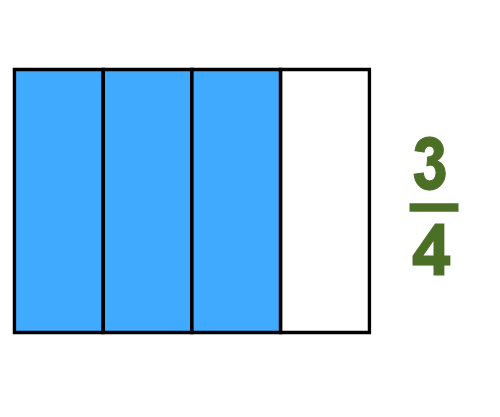
Equivalent fractions When you divide the same whole into different numbers of pieces, you can write the same proportion in different ways. For example, this whole is divided into 4 pieces, and 3 of them are shaded blue. In other words, we've shaded 3 quarters of the whole, or 3/4.
 Audio for slide 22 (mp3)
Audio for slide 22 (mp3)
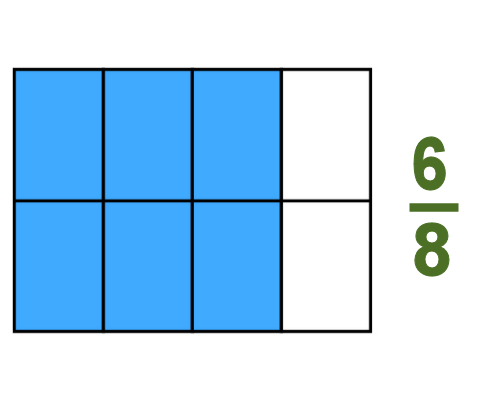
But if we divide the same whole into 8 pieces but still shade the same amount, we've now shaded 6 eighths of the whole, or 6/8. This means that 3/4 is equivalent to 6/8.
 Audio for slide 23 (mp3)
Audio for slide 23 (mp3)
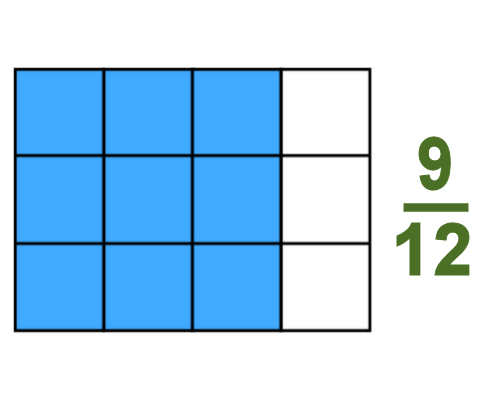
If we divide the original whole into 12 pieces, we'll have shaded 9 pieces. Therefore: 3/4 = 6/8 = 9/12 So if you were presented with the fraction 9/12, how would you know it was really the same proportion as 3/4?
 Audio for slide 24 (mp3)
Audio for slide 24 (mp3)
All you need to do is divide the top and bottom of the fraction by the same number. In this case, we know that 3 will divide evenly into both 9 and 12. That is: 9 ÷ 3 = 3 12 ÷ 3 = 4
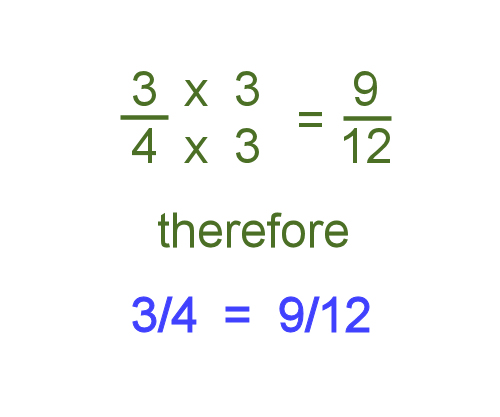 Audio for slide 25 (mp3)
Audio for slide 25 (mp3)
We can also run the calculation in reverse by multiplying both halves of the fraction by the same number. That is: 3 x 3 = 9 4 x 3 = 12
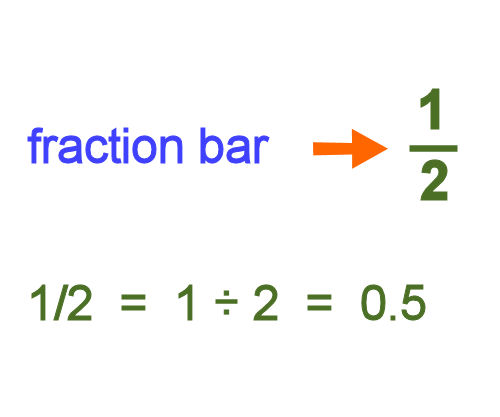 Audio for slide 27 (mp3)
Audio for slide 27 (mp3)
From fractions to decimals The fraction bar is like a division sign. For example, 1/2 is another way of saying: 1÷ 2. If you do this on your calculator, you will find that it equals 0.5. That is: 1÷ 2 = 0.5 To put it another way, 0.5 is the decimal equivalent of 1/2.
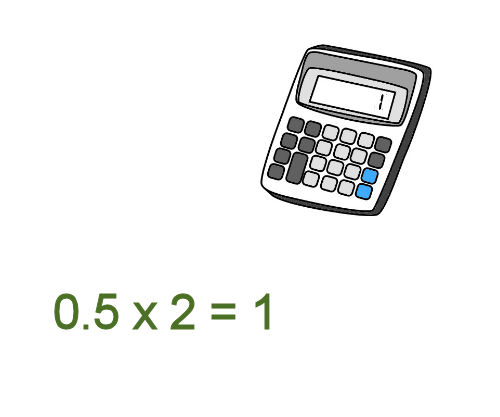 Audio for slide 28 (mp3)
Audio for slide 28 (mp3)
It's easy to confirm this answer by doing the calculation in reverse. That is, if 1/2 equals 0.5, then 0.5 times 2 should equal 1. You can check this on a calculator to prove it to yourself.
 Audio for slide 29 (mp3)
Audio for slide 29 (mp3)
In the same way, the fraction 1/4 is equivalent to the decimal 0.25. Again, you can check this on a calculator, and double-check it in reverse.
 Audio for slide 30 (mp3)
Audio for slide 30 (mp3)
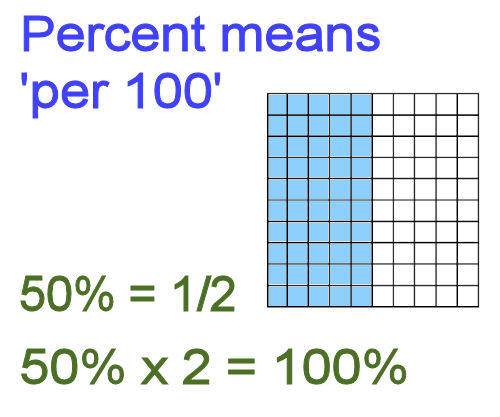
From fractions to percentages A percentage is simply another way of writing a fraction which has a denominator of 100. Per cent means 'per 100', or 'for every 100'. For example: 50% equals 50/100, which can be reduced to 1/2. So if 50% is the same thing as 1/2, then 50% x 2 should equal 100. And indeed it does!
 Audio for slide 31 (mp3)
Audio for slide 31 (mp3)
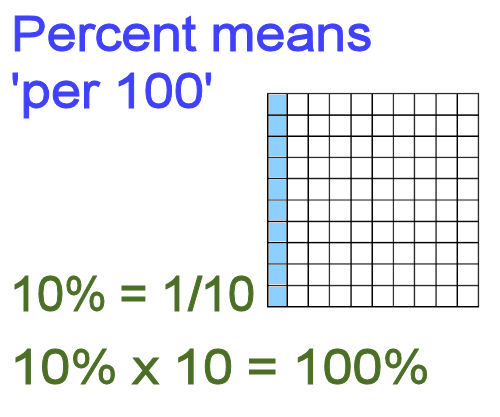
Here's another example: 10% = 10/100 = 1/10 This means that 10% x 10 = 100%
 Audio for slide 32 (mp3)
Audio for slide 32 (mp3)
Decimals and percentages Notice that percentages and decimals are basically the same thing. The only difference is: a percentage is a proportion of 100, and a decimal is a proportion of 1.
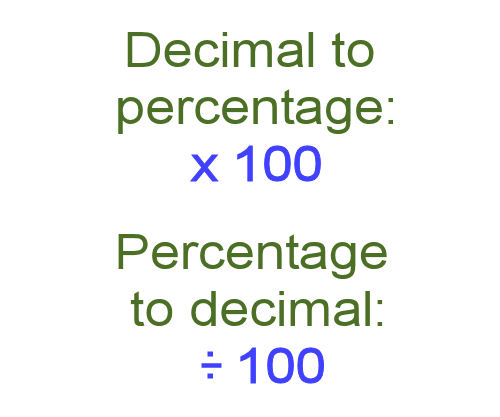 Audio for slide 33 (mp3)
Audio for slide 33 (mp3)
Therefore: to change a decimal to a percentage, multiply by 100, and to change a percentage to a decimal, divide by 100.
 Audio for slide 35 (mp3)
Audio for slide 35 (mp3)
Before the 1970s, the units of measure used in Australia generally came from the imperial system. This was a reference to 'imperial' Britain, because that's where the system was first developed. Length, for example, was measured in inches, feet, yards and miles. Weight was measured in ounces, pounds, stone and tons.
 Audio for slide 36 (mp3)
Audio for slide 36 (mp3)
However, between the 1970s and 1980s Australia progressively converted its measurement units across to the International System of Units - called the 'SI' (an abbreviation of the French 'Système International'). This is commonly referred to as the metric system.
 Audio for slide 37 (mp3)
Audio for slide 37 (mp3)
The metric system is based on the decimal system of numbers. This means that all measurement units are based on multiples of 10. For example, the standard unit of length is the metre. So the other units used to denote longer and shorter lengths are in multiples of 10 from the 'one metre' standard. Click on the link below to see the table of metric length units ranging from the millimetre (mm) to the kilometre (km). Table of metric lengths from mm to km
 Audio for slide 38 (mp3)
Audio for slide 38 (mp3)
As you look down this list of terms, you'll probably notice that not all of these units are commonly used. Metres and kilometres are terms used by just about everyone, including in ordinary day-to-day conversations. Millimetres are widely used in building, construction and manufacturing. Centimetres are also common in particular fields. But decimetres, decametres and hectometres have only limited usage in specialist areas.
 Audio for slide 39 (mp3)
Audio for slide 39 (mp3)
Nonetheless, the prefix (first half of the term) of each of these units is very handy to know, because it tells you what the quantity is in relation to the standard unit of measure, whatever it is that you're measuring.
 Audio for slide 40 (mp3)
Audio for slide 40 (mp3)
For example: Milli always means 1/1000, so: 1 millimetre (mm) is 1/1000 of 1 metre (m) 1 millilitre (mL) is 1/1000 of 1 litre (L) 1 milligram (mg) is 1/1000 of 1 gram (g)
 Audio for slide 41 (mp3)
Audio for slide 41 (mp3)
Kilo always means 1000, so: 1 kilometre (km) is 1000 metres 1 kilolitre (kL) is 1000 litres 1 kilogram (kg) is 1000 grams.
 Audio for slide 43 (mp3)
Audio for slide 43 (mp3)
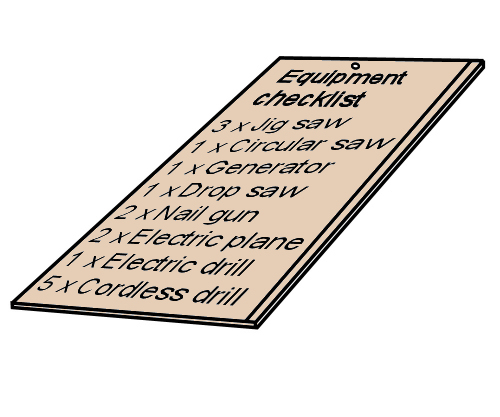
Tallies are used to record quantities of particular items or products. For instance, if you wanted to write down how many power tools you had taken onto a jobsite, your tally might read: 1 x jigsaw; 1 x circular saw; 3 x cordless drills; 2 x claw hammers ... and so on.
 Audio for slide 44 (mp3)
Audio for slide 44 (mp3)
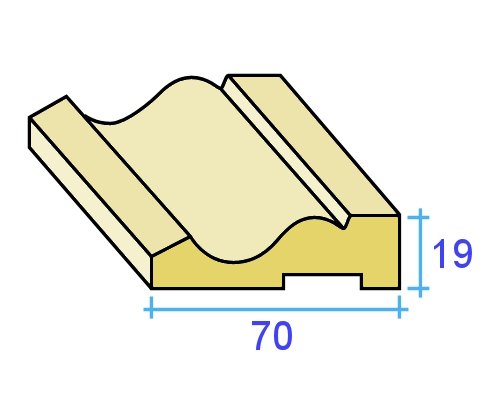
But if you had a product that was already expressed in terms of its cross-section size, such as 70 x 19 skirting board, it would get very confusing if you started to use the 'x' ('times') sign to also indicate the number and length of the pieces. Set out below are some examples of how to record tallies when you're working with items that are referred to by their cross sectional dimensions.
 Audio for slide 45 (mp3)
Audio for slide 45 (mp3)
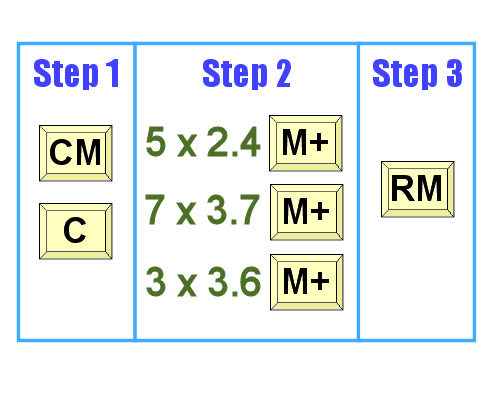
Example 1: skirting boards Let's say you have 15 pieces of skirting board, 70 mm x 19 mm in size. We'll say that 5 pieces are 2.4 metres in length, 7 pieces are 2.7 metres and 3 pieces are 3.6 metres. To show this as a tally, you would write it as follows: 70 x 19 skirting: 5/2.4, 7/2.7, 3/3.6 Now let's say we wanted to know how many lineal metres this tally represents. Note that 'lineal' means 'in a line' - so to put the question another way: What is the total metreage of these pieces if they were all laid out in a line?
 Audio for slide 46 (mp3)
Audio for slide 46 (mp3)
The easiest way to find the answer is to use a calculator with a memory button. Although not all calculators work in exactly the same way, the sequence of numbers and function buttons would be similar to that shown in the image. To see this process written out in more detail, click on the link below. Detailed description of calculation
 Audio for slide 47 (mp3)
Audio for slide 47 (mp3)
If you don't have a calculator with a memory button, you can simply multiply each line separately and then add the subtotals together, as shown in this image.
 Audio for slide 48 (mp3)
Audio for slide 48 (mp3)
Example 2: plywood sheets Sheet materials sometimes have their dimensions shown in metres and sometimes in millimetres. For example, if you had two sheets of ply that were 9 mm thick, 2.4 metres long and 1.2 metres wide, it could be written up as follows: 9 mm ply: 2 / 2.4 x 1.2 or alternatively: 9 mm ply: 2 / 2400 x 1200
 Audio for slide 50 (mp3)
Audio for slide 50 (mp3)
Now that we've covered the main terms used in the metric system and looked at the relationship between fractions, decimals and percentages, it's time to apply these principles to some workplace calculations.
 Audio for slide 51 (mp3)
Audio for slide 51 (mp3)
In this section, we'll start with measurements of length, and work up to volume calculations for three dimensional shapes. We'll also talk about methods of checking angles. And we'll introduce some of the measuring instruments used in laying floor coverings and discuss ways of making sure that the measurements you take with them are reliable and accurate.
 Audio for slide 53 (mp3)
Audio for slide 53 (mp3)
In the previous section we talked about the metric system, and used the units of length to show how the different prefixes relate to each other - such as kilo-, deci-, centi- and milli-. Floor layers use millimetres for most measurements. However, this hasn't always been the case - see 'Understanding measurements' in the unit Planning and costing for more details on the different units of measure that are used in floor laying.
 Audio for slide 54 (mp3)
Audio for slide 54 (mp3)
In cases where thicknesses of less than a millimetre are used, such as when manufacturers state the thickness of a flooring product's wear layer, the unit of measure often used is the micrometre. One micrometre is 1/1,000,000 (one millionth) of a metre, or 1/1,000 (one thousandth) of a millimetre. Its symbol is ' µm', which is sometimes written as 'um'.
 Audio for slide 55 (mp3)
Audio for slide 55 (mp3)
Many people prefer to use the old fashioned term micron instead of micrometre. This is designed to avoid confusion with the measuring device called the micrometer, although strictly speaking 'micron' is no longer officially recognised as a term under the SI system. In practice, micrometres are often expressed as millimetres to several decimal places. For example, 500 µm might simply be referred to as 0.5 mm, and 50 µm would be 0.05 mm.
 Audio for slide 56 (mp3)
Audio for slide 56 (mp3)
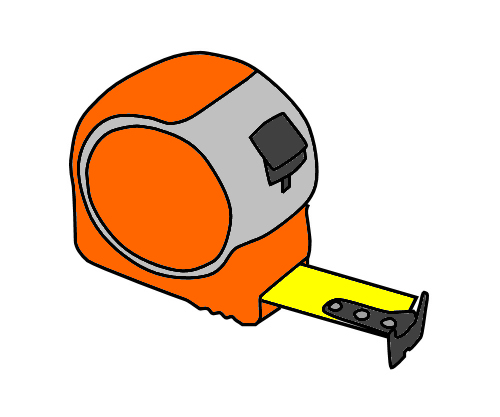
Measuring devices The most common general-purpose measuring device is the tape measure. Spring loaded retractable tape measures range in length from tiny 1 metre tapes to the standard 7 to 8 metre tradesperson's tape.
 Audio for slide 57 (mp3)
Audio for slide 57 (mp3)
When you look closely at the end of a normal retractable tape, you'll notice that the steel hook is secured with rivets, with a bit of play in the holes allowing it to move back and forth. The amount of movement allowed is the same as the thickness of the hook. Its purpose is to compensate for the hook thickness when you either push the tape up against an object for an inside measurement or hook it over the object for an outside measurement.
 Audio for slide 58 (mp3)
Audio for slide 58 (mp3)
Other common measuring devices are as follows: Steel rule - very rugged, good for fine measurements, able to be used as a straight edge.
 Audio for slide 59 (mp3)
Audio for slide 59 (mp3)
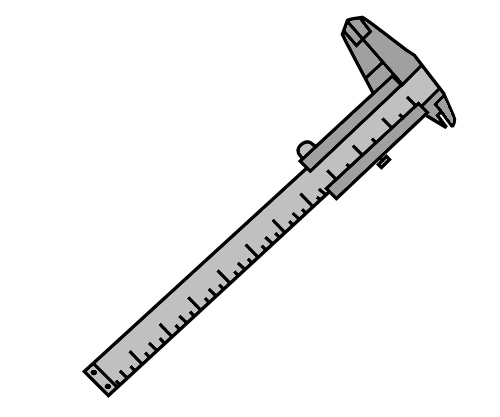
Vernier caliper - used for measuring thicknesses and diameters very precisely, in some cases to an accuracy of 10 micrometres, or 0.01 mm.
 Audio for slide 60 (mp3)
Audio for slide 60 (mp3)
Laser distance meter - measures digitally with a laser beam; can be either hand held or combined with a laser level.
 Audio for slide 62 (mp3)
Audio for slide 62 (mp3)
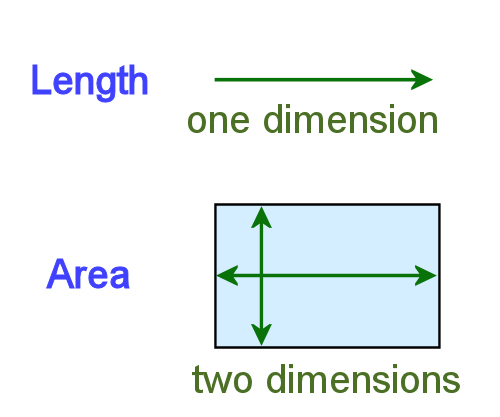
If you think of length as being one dimensional, that is, going in one direction only, then area is two dimensional, because it has length and width. Let's have a look at the area of some common shapes.
 Audio for slide 63 (mp3)
Audio for slide 63 (mp3)
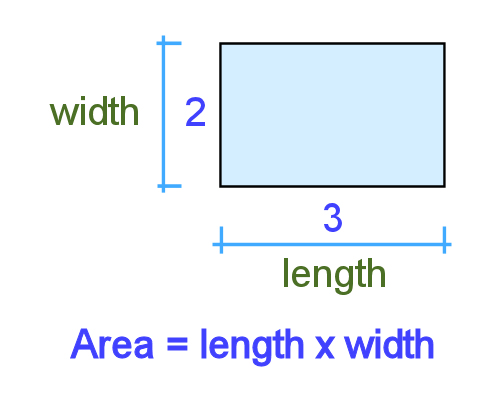
Squares and rectangles The area of any square or rectangle is simply its length times its width. For example, if a rectangle is 3 metres long and 2 metres wide, its area is: Length x width = 3 m x 2 m = 6 square metres (m²)
 Audio for slide 64 (mp3)
Audio for slide 64 (mp3)
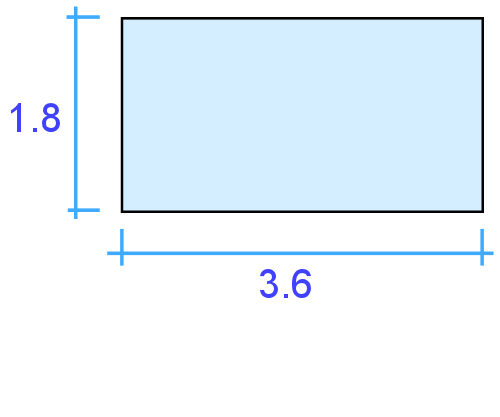
What if you had a sheet of particleboard measuring 3.6 m x 1.8 m? Its area is simply: Length x width = 3.6 m x 1.8 m = 6.48 m²
 Audio for slide 65 (mp3)
Audio for slide 65 (mp3)
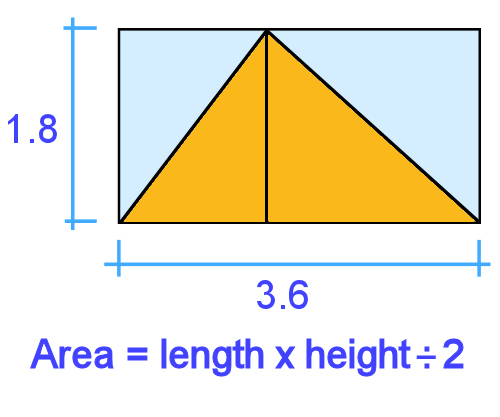
Triangles Let's say you cut the sheet of particleboard in half diagonally, forming two equal triangles. The area of each triangle is exactly half of the original rectangle. That is: Length x height ÷ 2 = 3.6 x 1.8 ÷ 2 = 3.24 m²
 Audio for slide 66 (mp3)
Audio for slide 66 (mp3)
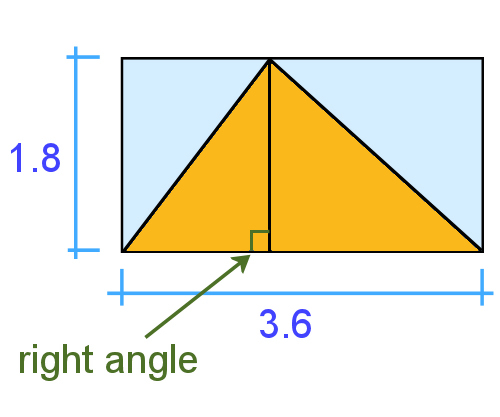
This proves that a triangle is half the area of the rectangle or square that it came from. So even if you had a triangle that didn't have a right angle in it, the calculation is still the same, because you could simply divide the triangle into 2 triangles, and the rectangle around it into 2 rectangles.
 Audio for slide 67 (mp3)
Audio for slide 67 (mp3)
But note that you must always measure the height of the triangle at right angles (90 degrees) to the base. You can't measure the diagonal line in the triangle, because that's not the true height of the rectangle that goes around it.
 Audio for slide 68 (mp3)
Audio for slide 68 (mp3)
Circles You may remember from your school days that the formula for the area of a circle is: Π r², where Π is 3.14, and 'r' is the radius of the circle.
 Audio for slide 69 (mp3)
Audio for slide 69 (mp3)
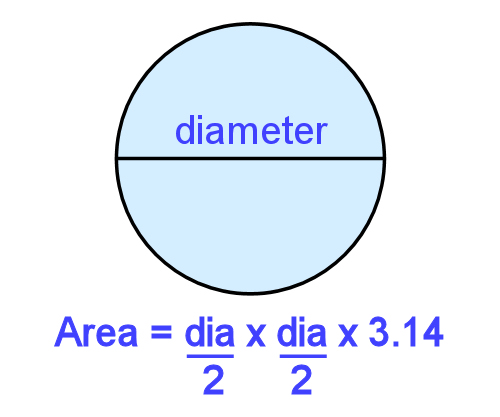
If you're happy using that formula you can stay with it, but you might prefer this simplified version - which is actually the same, but just put in different terms: Area of a circle = diameter x diameter x 3.14 2 2 Another way of writing this is: Area = (diameter ÷ 2) x (diameter ÷ 2) x 3.14
 Audio for slide 70 (mp3)
Audio for slide 70 (mp3)
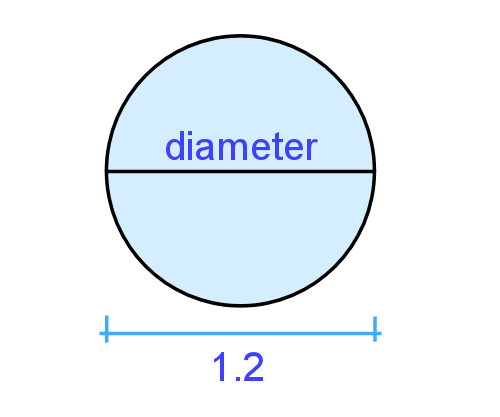
Here's an example. If a circle is 1.2 m in diameter, what's its area? The answer is shown below. Area = (diameter ÷ 2) x (diameter ÷ 2) x 3.14 = (1.2 ÷ 2) x (1.2 ÷ 2) x 3.14 = 0.6 x 0.6 x 3.14 = 1.13 m²
 Audio for slide 71 (mp3)
Audio for slide 71 (mp3)
So where does 3.14 come from? This is actually the approximate ratio between the circumference, or outside measurement, of the circle and its diameter. In other words, the circumference of a circle is roughly 3.14 times longer than its diameter.
 Audio for slide 72 (mp3)
Audio for slide 72 (mp3)
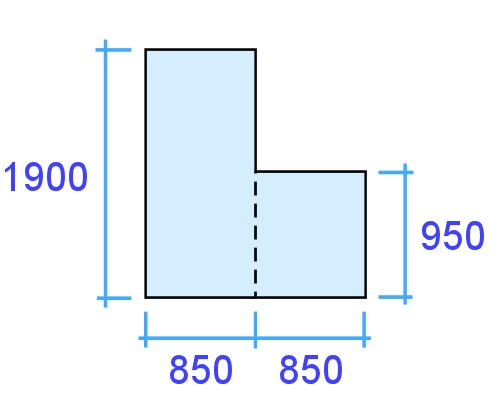
Compound shapes If you can break a shape up into its basic parts, you can calculate its area by adding the separate areas together. Example 1: L shape This L shape is basically two rectangles. What is its area? Note that the measurements in the diagram are shown in millimetres, so you'll need to convert them into metres for the calculation. A good way to set out the workings is as follows. Rectangle 1: 1.9 x 0.85 = 1.615 m² Rectangle 2: 0.95 x 0.85 = 0.808 m² Total area: 1.615 + 0.808 = 2.423 m² Written mathematically, this would be: (1.9 x 0.85) + (0.95 x 0.85) = 2.423 m²
 Audio for slide 73 (mp3)
Audio for slide 73 (mp3)
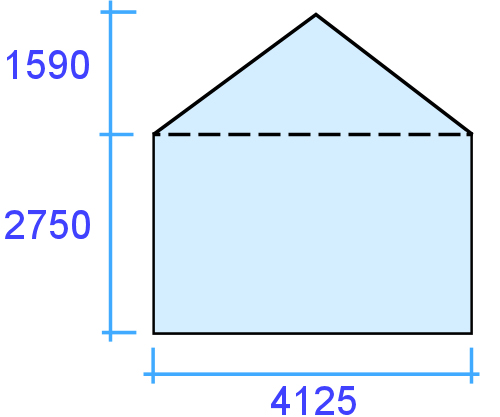
Example 2: Gable end of a house This shape is a triangle plus a rectangle. Again, you can set out your workings in the same way. Triangle: 1.59 x 4.125 ÷ 2 = 3.279 m² Rectangle: 2.75 x 4.125 = 17.05 m² Total area: 5.58 + 17.05 = 22.63 m² Written mathematically: (1.8 x 6.2 ÷ 2) + (6.2 x 2.75) = 22.63 m²
 Audio for slide 74 (mp3)
Audio for slide 74 (mp3)
. Example 3: Half circle around a bay window This floor area is made up of a rectangle and a semicircle. The formulas and calculations for finding this area are as follows: Semicircle area = area of circle ÷ 2. In other words: Semicircle = (diameter ÷ 2) x (diameter ÷ 2) x 3.14 ÷ 2 = (3.3 ÷ 2) x (3.3 ÷ 2) x 3.14 ÷ 2 = 1.65 x 1.65 x 3.14 ÷ 2 = 4.274 m2 Now we can do the rest of the calculation: Rectangle: 6.0 x 3.3 = 19.8 m2 Total area: 4.274 + 19.8 = 24.074 m2 Written mathematically: (3.3 ÷ 2 x 3.3 ÷ 2 x 3.14 ÷ 2) + (6.0 x 3.3) = 24.074 m2
 Audio for slide 76 (mp3)
Audio for slide 76 (mp3)
When two straight lines meet, they form an angle between them. If the lines are walls in a square room, or the sides of a square box, they will form a right angle.
 Audio for slide 77 (mp3)
Audio for slide 77 (mp3)
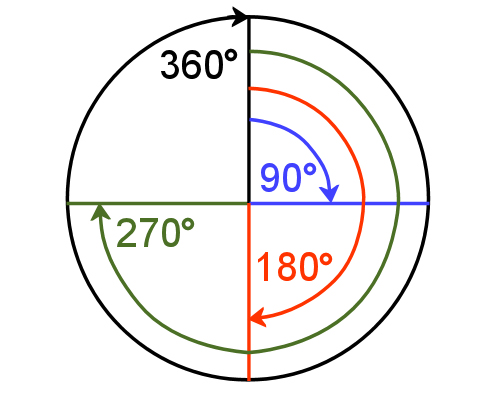
Another way of referring to a right angle is to say it is 90° (degrees). This is a reference to the amount of turn between the 2 lines. That is, if you had a circle and drew a radius from the middle to the top, and then rotated it one quarter of a turn, you would have turned the radius through 90°. One full turn around a circle is 360°. This means that every angle formed between the two lines will be something less than that - for example, one quarter is 90°, half is 180°, three quarters is 270°.
 Audio for slide 78 (mp3)
Audio for slide 78 (mp3)
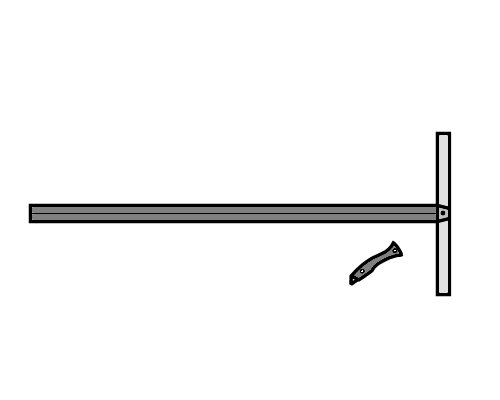
Setting out and marking lines at angles The most common tools used by flooring installers to draw lines, set out angles and guide a utility knife while cutting are as follows. Straight edge square, used for long lines at right angles to an edge.
 Audio for slide 79 (mp3)
Audio for slide 79 (mp3)
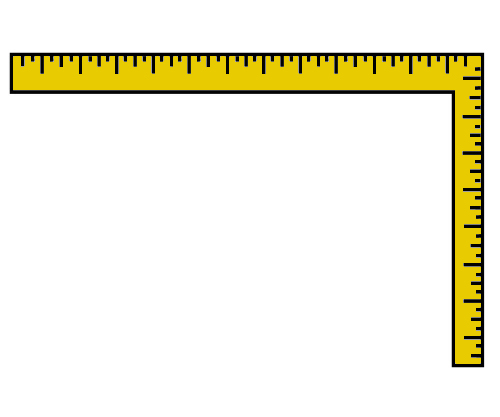
Carpenter's square, also called a builder's square, used for right angles and for measuring.
 Audio for slide 81 (mp3)
Audio for slide 81 (mp3)
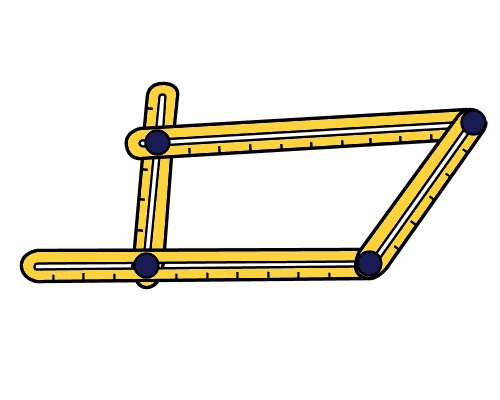
Template tool, which can be used to transfer angles from the installation area onto the floor covering material.
 Audio for slide 82 (mp3)
Audio for slide 82 (mp3)
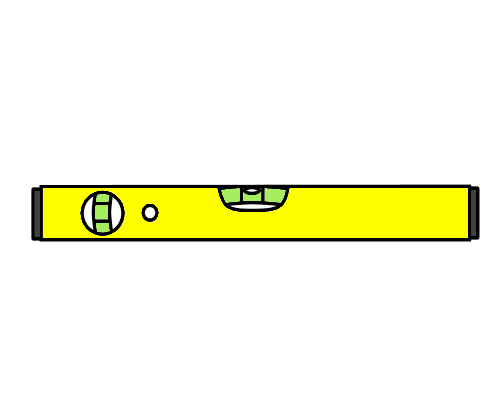
Using a level Level means perfectly horizontal. A spirit level allows you to check that a surface or line is horizontal. It works on the principle that the bubble will find the highest point in a glass tube, because it is lighter than the surrounding fluid.
Since the tube is curved slightly with the highest point in the middle, the bubble floats exactly in the middle when the level is horizontal.
Since the tube is curved slightly with the highest point in the middle, the bubble floats exactly in the middle when the level is horizontal.
 Audio for slide 83 (mp3)
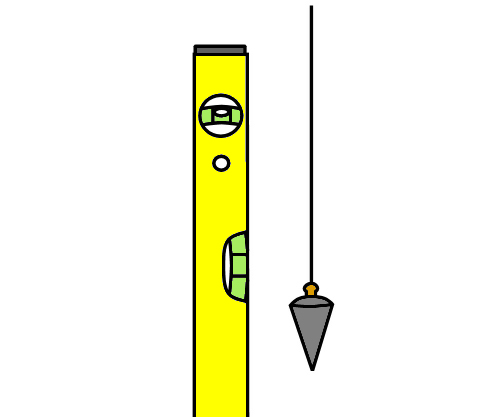
Audio for slide 83 (mp3)
You can also use a level to check whether a surface or line is plumb. 'Plumb' means perfectly vertical, and comes from a Latin word meaning 'lead'. This is a reference to the plumb bob, which traditionally was always made of lead. When a plumb bob is hung from a string, gravity draws the weight downwards, and the string forms a vertical line.
 Audio for slide 84 (mp3)
Audio for slide 84 (mp3)
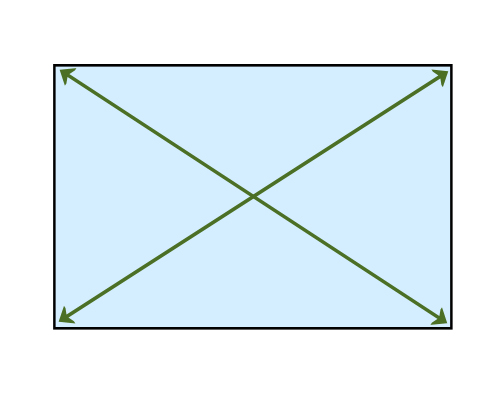
Measuring diagonals One way of checking to see whether a square or rectangular shape has right angled corners is to measure the diagonals. This principle works because the opposite sides of a square or rectangle are always parallel - that is, the same distance apart at both ends. Therefore, if the corners are at 90°, or 'square', the two diagonals will be the same length.
 Audio for slide 85 (mp3)
Audio for slide 85 (mp3)
If the diagonals are not the same length, then the corners can't be square, even if the sides are still parallel. It's worth keeping this in mind as a reminder that you can't simply measure the lengths of the sides to check that an item is square - this won't tell you whether the corners are at right angles.
 Audio for slide 86 (mp3)
Audio for slide 86 (mp3)
Using the 3, 4, 5 rule Another way of checking a corner for square is to use the 3, 4, 5 rule. This is an application of an old formula that Pythagoras, the ancient Greek philosopher, came up with over 2,500 years ago.
 Audio for slide 87 (mp3)
Audio for slide 87 (mp3)
Let's say you wanted to check whether the walls in the corner of a room were square, but it was a big open-plan room that didn't have opposite corners to measure. The 3, 4, 5 rule states that if you measure 3 units along one wall and mark the point, and 4 units along the other wall and mark the point, the distance between the two points should be 5 units if the corner is square. It doesn't matter what length a 'unit' is, as long as the proportions are 3, 4 and 5. That is, your lengths could be 3 metres, 4 metres, 5 metres; or 3 feet, 4 feet, 5 feet; or 6, 8, 10 or any other multiple of 3, 4, 5.
 Audio for slide 89 (mp3)
Audio for slide 89 (mp3)
So far we've described length as being one dimensional and area as two dimensional. But for an object to take up space in the real world it needs a third dimension. Volume is a way of measuring three dimensional space.
 Audio for slide 90 (mp3)
Audio for slide 90 (mp3)
We know that if a square measures one metre by one metre, it will have an area of one square metre (m2). If we now give it a depth of one metre, it will have a volume of one cubic metre (m3). This is the standard unit of volume in the SI metric system.
 Audio for slide 91 (mp3)
Audio for slide 91 (mp3)
Here are some metric volume measurements: 1 cubic metre (m3) = 1,000 litres (L) = 1,000,000 cubic centimetres (cm3) 1 L = 1,000 millilitres (mL) = 1,000 cm3 1 mL = 1 cm3
 Audio for slide 92 (mp3)
Audio for slide 92 (mp3)
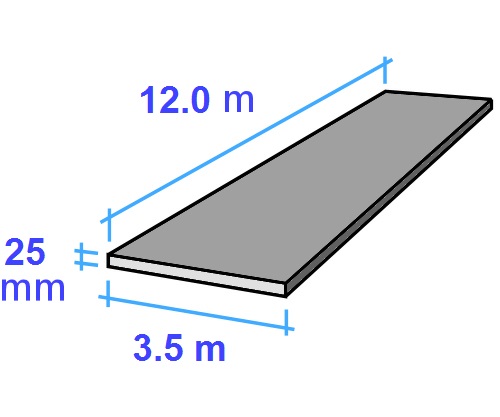
Example 1: Concrete slab How much cement-based filler do you need to lay on top of a concrete subfloor if the average thickness is going to be 25 mm and the slab measures 12 m by 3.5 m? Notice that there is a combination of units here - the length and width are in metres and the thickness is in millimetres. So the first thing we need to do is convert the thickness to metres: 25 mm = 0.025 m3 Now we can do the calculation. Volume = length x width x thickness = 12 m x 3.5 m x 0.025 m = 1.05 m3 In practice, you might add 10% to cover variations in the original subfloor level which will affect the thickness of your filler. So in this case you would add 0.105 m3 to the total.
 Audio for slide 93 (mp3)
Audio for slide 93 (mp3)
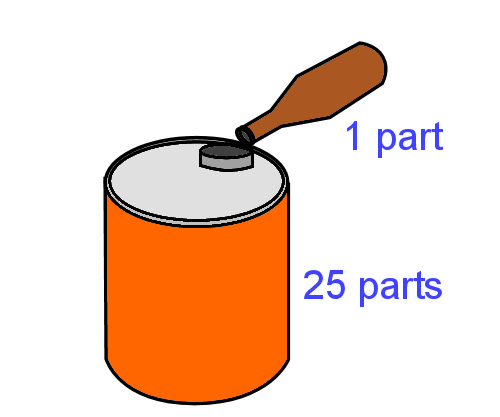
Example 2: 2-stroke fuel A common petrol:oil ratio for 2-stroke engines is 25:1. This means that for every 25 parts of petrol you need to mix in 1 part of 2-stroke oil. If you had a 4 litre container of petrol, how much oil do you need to add? We know that: 1 L = 1000 mL, so 4 L = 4,000 mL. Therefore the calculation will be as follows. 4,000 mL (petrol) ÷ 25 = 160 mL (2-stroke oil).
 Audio for slide 94 (mp3)
Audio for slide 94 (mp3)
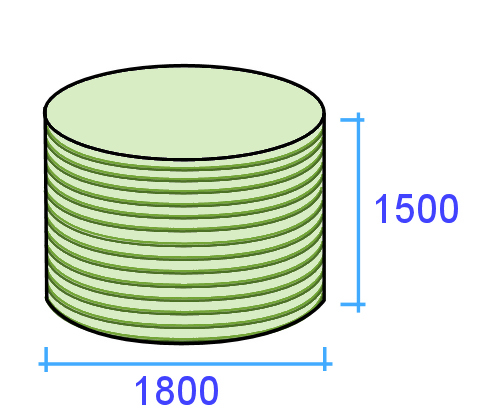
Example 3: Water tank How much water can a tank hold with a diameter of 1800 mm and a height of 1500 mm? Here is the calculation. Cylinder volume = area of circle (cross section) x height = diameter x diameter x 3.14 x height 2 2 = 1.8 ÷ 2 x 1.8 ÷ 2 x 3.14 x 1.5 = 0.9 x 0.9 x 3.14 x 1.5 = 3.815 m3 Since there are 1000 litres in 1 m3, the volume in litres is: 3.815 m3 x 1000 = 3815 L
 Audio for slide 96 (mp3)
Audio for slide 96 (mp3)
Throughout this unit we've touched on a few issues that can cause errors in measurements and calculations. The suggestions we've provided so far for avoiding errors include: writing down the numbers first, especially if someone else is calling them out to you, so that you have a written record of the measurements or quantities estimating the answers you would expect to see in a calculation, so that if there's a glaring error you can pick it up more easily reading the numbers and graduations carefully on a tape measure, to make sure that you're taking off the correct measurement from the correct section of the tape. Below are some more suggestions for making sure that the measurements you take are accurate and correct.
 Audio for slide 97 (mp3)
Audio for slide 97 (mp3)
Reading dials and gauges A common error when reading dials or gauges is to look at the pointer from an angle to the scale. This means that instead of reading off the mark immediately behind the pointer, you read a mark that is either on the left or right hand side of the pointer. The problem is called parallax error, because 'parallax' refers to the way an object seems to change its position when your own point of observation changes.
 Audio for slide 98 (mp3)
Audio for slide 98 (mp3)
Some instruments have a mirror on the dial so that you can line up the pointer with its own reflection, to make sure that your reading is exactly at right angles to the scale. Even if there isn't a mirror, the simple solution to the problem is to use one eye only and make sure you're looking at the scale at exactly 90 degrees.
 Audio for slide 99 (mp3)
Audio for slide 99 (mp3)
It is even possible to get a parallax error with a ruler or tape measure if the graduations are not hard against the mark or edge that you want to measure. Again, always make sure that your eye is at 90 degrees to the scale when you take the measurement. In the case of the tape measure, you should also push down the steel blade so that the edge you're reading from is flat against the object being measured.
 Audio for slide 100 (mp3)
Audio for slide 100 (mp3)
Calibrating instruments Some measuring instruments need to be calibrated before they are used. This often means resetting the zero mark or testing the instrument against a benchmark reading.
 Audio for slide 101 (mp3)
Audio for slide 101 (mp3)
Some instruments also need to be adjusted differently for particular types of materials. For example, moisture meters for timber use different scales depending on the species of hardwood or softwood being measured. The simplest way of making these sorts of allowances is to have a conversion chart that enables the user to add or subtract amounts to give a 'corrected' reading.
 Audio for slide 102 (mp3)
Audio for slide 102 (mp3)
'Measure twice, cut once' This is an old saying that just about every apprentice or worker has heard from their boss. It's a good saying, because it's a little reminder that simple mistakes can happen any time, and they're easy to fix if all that's needed is another quick check.
 Audio for slide 103 (mp3)
Audio for slide 103 (mp3)
But once you've cut the piece or committed yourself in some other way to the measurement you've just taken, it may end up being a very big mistake if your measurement turned out to be wrong. In that sense, the extra time taken to double-check a measurement or calculation is time very well spent, because at the very least it will give you the confidence that you were right the first time. And if it does happen that your second reading is different from the first one, you'll have given yourself a get-out-of-jail-free card, because you can immediately correct the error before it causes you any grief or expense.